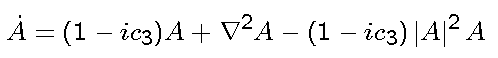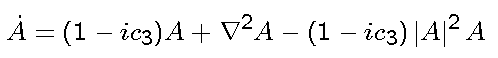| Relaxational Ginzburg Landau Equation |
|
Plot type 1 shows the magnitude of the complex field is plotted on a gray scale minimum-maximum = black-white.
Plot type 2 shows the phase angle plotted on a "rainbow" color plot 0-90-180-270-360 = red-yellow-green-blue-red.
The simulation evolves the equation for the complex field A(x,y,t):
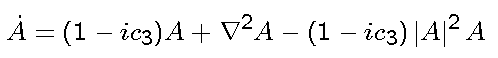
from random initial conditions.
For c3=0 the equation describes the dynamics of a relaxational the XY model such as the thin film nematic, and at low temperature where there is essentially zero probability of thermally exciting vortex pairs (there is no noise corresponding to thermal fluctuations in the simulation). The random initial conditions would correspond to starting from the high temperature disordered state, i.e., to a temperature quench in a physical system. In plot type 1, showing |A|, the dark spots are the centers of the vortices. In plot type 2, showing the phase of A, the rainbow of colors circling these centers is the phase winding. Unlike vortices attract each other, and slowly move together and annihilate, leaving the uniform ordered state. This type of quench, and the subsequent dynamics of the topological defects is of interest in many systems, including superfluids and models of the early universe (do a Google or other search on Kibble mechanism. I found, for example, this link.
We'll return to the case of c3 nonzero later.
Last modified March 28, 2006
Michael Cross