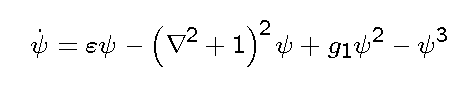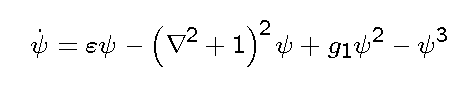Swift-Hohenberg Equation - Strong Nonlinearity
This demonstrations illustrates how that different patterns result from different initial conditions (here random) at strong nonlinearity. Reduce eps and see if the final pattern is the same from run to run.
The equation
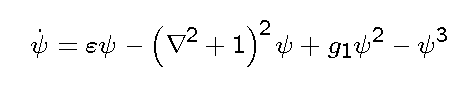 is solved in a square of side 64. The initial condition is random with the value at each point of the mesh chosen from a uniform distribution between +/-0.005. The discrete mesh for the numerical evolution is 64x64 and the results are interpolated onto a mesh 256x256 for plotting.
Demonstrations-1-2
is solved in a square of side 64. The initial condition is random with the value at each point of the mesh chosen from a uniform distribution between +/-0.005. The discrete mesh for the numerical evolution is 64x64 and the results are interpolated onto a mesh 256x256 for plotting.
Demonstrations-1-2