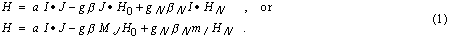
Experiment 6
September 1994
Electron Spin Resonance (ESR), often called Electron Paramagnetic Resonance (EPR), is similar to Nuclear Magnetic Resonance (NMR), the fundamental difference being that ESR is concerned with the magnetically induced splitting of electronic spin states, while NMR describes the splitting of nuclear spin states. In both ESR and NMR, the sample material is immersed in a strong static magnetic field and exposed to an orthogonal low- amplitude high-frequency field. ESR usually requires microwave-frequency radiation (GHz), while NMR is observed at lower radio frequencies (MHz). With ESR, energy is absorbed by the sample when the frequency of the radiation is appropriate to the energy difference between two states of the electrons in the sample, but only if the transition satisfies the appropriate selection rules. Splitting can occur only when the electron is in a state with non-zero total angular momentum, i.e. electrons in atoms with closed atomic shells cannot show this behavior. The term ESR refers specifically to the case in which the spins of the electrons absorbing the radiation are only weakly interacting ("weakly coupled") with each other. In NMR the static magnetic field splits the quantum states of a nucleus which has non-zero nuclear spin. The observation of NMR requires that the total electronic spin be zero. Why? (Read Feynman's discussion of NMR, Vol. 2, 35-6.)
Our experiment makes use of a bulk sample (as contrasted to Rabi's molecular beam resonance method discussed in Feynman), and is limited to those materials that have electrons with non-zero total angular momentum (or a "dipole moment"). Because of chemical binding, most materials in bulk form do not have net electronic angular momentum, and thus are not suitable for this experiment. Some materials which are suitable are:
If a paramagnetic atom or molecule is placed in a solid there will be interactions between it and its surroundings. In the case we will examine, the result of these interactions will be to leave the single paramagnetic electron in a state which appears similar to that of an s - state electron, which has zero orbital angular momentum and therefore allows us to examine the effect of a magnetic field on the spin motion.
The paramagnetic atom or molecule has a quantum state determined by the Hamiltonian, which contains several terms. The dominant potential term is the Coulomb interaction between the paramagnetic electron and the electrons of its own atom, the neighboring atoms, and the positive charges of its own nucleus. This large Coulomb interaction defines the basic ground state for the electron. The remaining terms can be considered as perturbations.
Assuming that the effect of the Coulomb terms has been to leave this electron in an L=0 (quenched orbital motion) state, the magnetic perturbation Hamiltonian can be written:
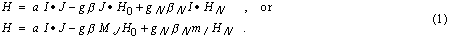
The total electron angular momentum quantum number J is just the spin quantum number, S, in this case. The nuclear angular momentum quantum number I is determined by the net spin of the nucleus. The first term is the hyperfine interaction, and in this case (L = 0) is the "Fermi Contact" term. The second term is the electronic Zeeman term due to the effect of the applied magnetic field H0 on the electron spin. The third term is the nuclear Zeeman term due to the effect of the magnetic field on the nuclear spin. Since beta_N is much smaller than beta, this last term is small. The magnetic field H_N seen by the nucleus may be modified by the electron system. Beta and beta_N are the electron and nuclear "magnetons" beta = e h / (4 pi mc).
The electron's 'g' factor is given by the Lande rule for the vector model of the atom. The nuclear 'g' factor, g_N, is obtained from a knowledge of the structure of the nucleus.
With fields of the magnitude used in this experiment (several kiloGauss), F = I + J is not a good quantum number. Energy splittings due to the applied field are comparable to, or larger than, the energy splittings between different F states. Put another way, the states of total F are "mixed" by the applied field, and thus F is not a good description of the state of the system. However, J = L + S is a good quantum number, for even at fields of the magnitude used here, the spin-orbit splitting is much greater than the splitting due to the applied field.
Thus the good quantum numbers for use in this experiment are J and I, and their projections along the field axis. The energy levels of a paramagnetic ion in a magnetic field of the magnitude available to this experiment will be dependent on the values of M_J and M_I, as illustrated for Mn++ in Figure 1.
Mn++ is the manganese atom with two 'd' electrons missing from the 3d shell. This leaves 5 electrons in the 3d shell (half filled). The ground state for this case is that in which all 5 electron spins are parallel, i.e.,6S_5/2. Since the nuclear spin I = 5/2, the total quantum number F = I + S (since L = 0), ranges from 0 to 5. Figure 1 shows the splitting of just the S = 1/2 component. The other spin components will split more rapidly with magnetic field than does the S = 1/2 component, but the allowed transitions will be degenerate with those for S = 1/2, so only 6 lines will be seen in the spectrum.
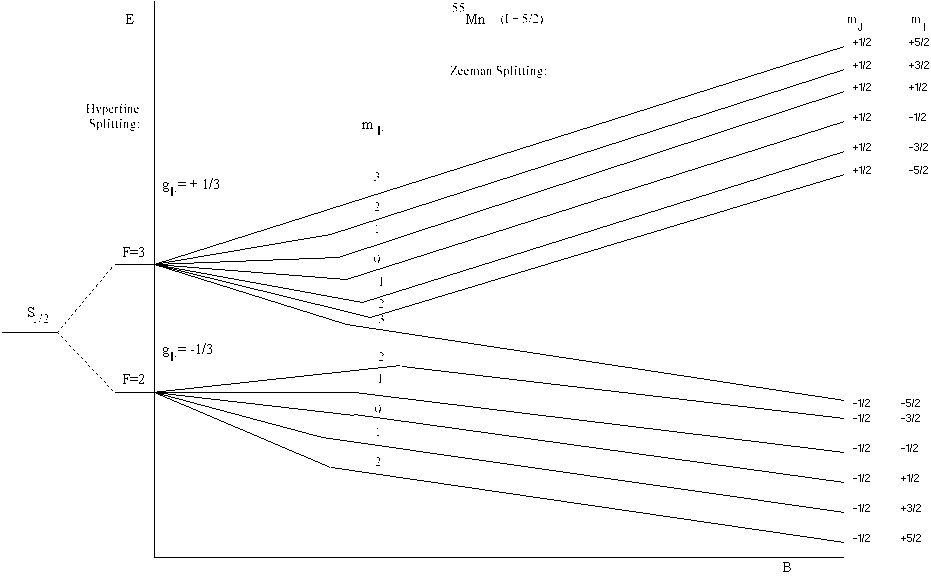
S=1/2. L=0, J=1/2, I=5/2
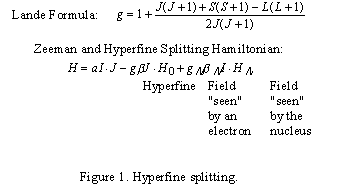
The width of the absorption peak in ESR is very much greater than in NMR. This width arises from the spin-spin interaction between neighboring atoms. In a sample containing N spins per cm^3 (e.g., N DPPH molecules per cm^3 with one unpaired electron per molecule), each acting as a dipole of strength m, the field H at any spin is the sum of the applied field plus that due to neighboring spins:

Spins throughout the sample see a field varying between H_0 + mu N and H_0 - mu N, giving rise to a "line width", just as if the external field were non-uniform. For nuclear spins we find that:

while for electronic spins;
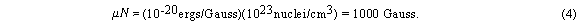
The breadth of the ESR lines makes them difficult to observe unless the applied field is quite large. (Why not reduce N?)
In some materials, DPPH for one, the line will not be this broad. In DPPH, the single unpaired electron wave function extends over the entire volume of the molecule, which is about 10^-7cm in diameter. Furthermore, in a solid material, the exchange integral between neighboring molecules is large, and the electron is shared between neighboring molecules, as in the hydrogen bond. This gives rise to "exchange narrowing", a quantum phenomenon first described by Van Vleck (Phys. Rev., 74, 1168 (1948)). This "exchange narrowing" might also be called "migration narrowing", and can be pictured classically by supposing that the electron is smeared over a large region of many molecules. It sees an average H field, averaged over many molecules, with fluctuations averaged to zero, leaving only the applied field. Support for this explanation will be found in the fact that, in a dilute solution of DPPH, the resonance line becomes broader, presumably because the exchange integral is reduced due to increased inter-molecular spacing. In DPPH crystals, such as you will use, the line width is about 2.7 Gauss.
This consists of an electromagnet with power supplies to generate and modulate a uniform magnetic field of several thousand Gauss, as well as the components that generate and detect microwaves.
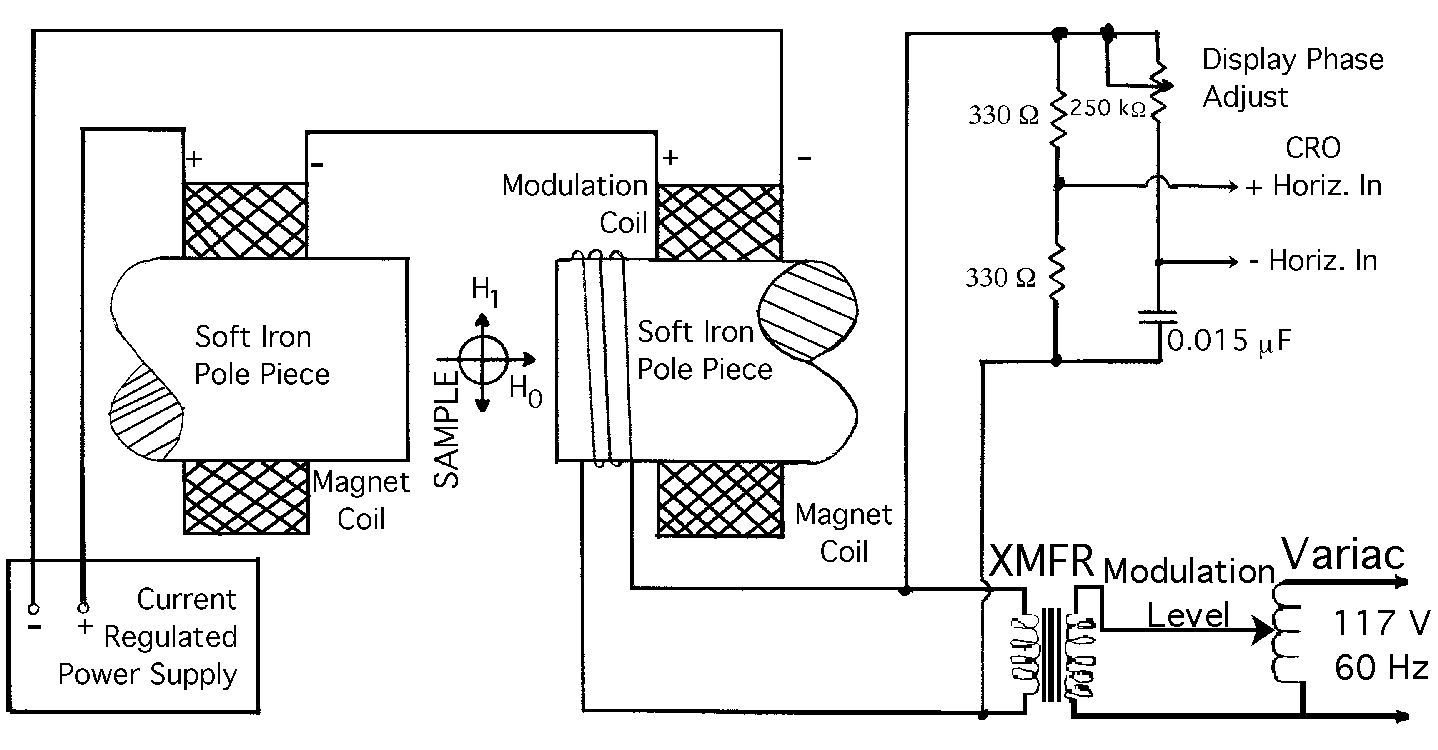
Figure 2. An ESR Spectrometer showing the sample, magnetic fields applied to it, and the sources of these fields.
A static magnetic field is provided by a 10 cm diam. electromagnet with a current- regulated power supply (15 A Maximum). A 60 Hz AC component is added to this field by an adjustable current through a winding on one pole piece of the electromagnet. A voltage that is proportional to the amplitude of this modulation provides the horizontal display for the CRO, with provision for shifting the phase between the signal delivered to the CRO and the modulation applied to the main magnetic field. As with an NMR experiment, a homogeneous field is required for best results.
A Hall device, driven from a stable constant-current power system, with a digital multimeter (DMM) reading the Hall voltage, is used to measure the average value of the magnetic field applied to the ESR samples. The drive current has been set to make the device direct-reading with an error of < ± 3%, providing that the temperature of the Hall device does not deviate significantly from normal (19-25 oC). The DMM must be set to its 200 mV range (1 microV least significant digit) and carefully "zeroed". Ignore the decimal point. The change in the least significant figure will then be 1 Gauss. When making a measurement place the probe as close to the microwave cavity wall as possible and away from the warm magnet pole face.
The microwave system is contained entirely within the gap of the electromagnet. See Figure 3. It consists of a short length of Ku (RG-53) rectangular waveguide (12 GHz), short circuited at both ends to provide a relatively high-Q resonant cavity. The samples to be investigated are mounted slightly off center on a rotatable cylindrical plug whose end surface is flush with one end of the cavity. This allows the samples to project slightly into the microwave field of the cavity and their positions to be optimized for best signal-to-noise ratio. A microwave Gunn diode is mounted along the center of the long axis of the cavity, approximately 1/3 of the cavity length from the end opposite the samples. The diode spans the short dimension of the rectangular waveguide, efficiently coupling to the E vector of the microwave field, resulting in maximum efficiency both in generating microwaves and in simultaneously detecting the influence on that field by samples at resonance.
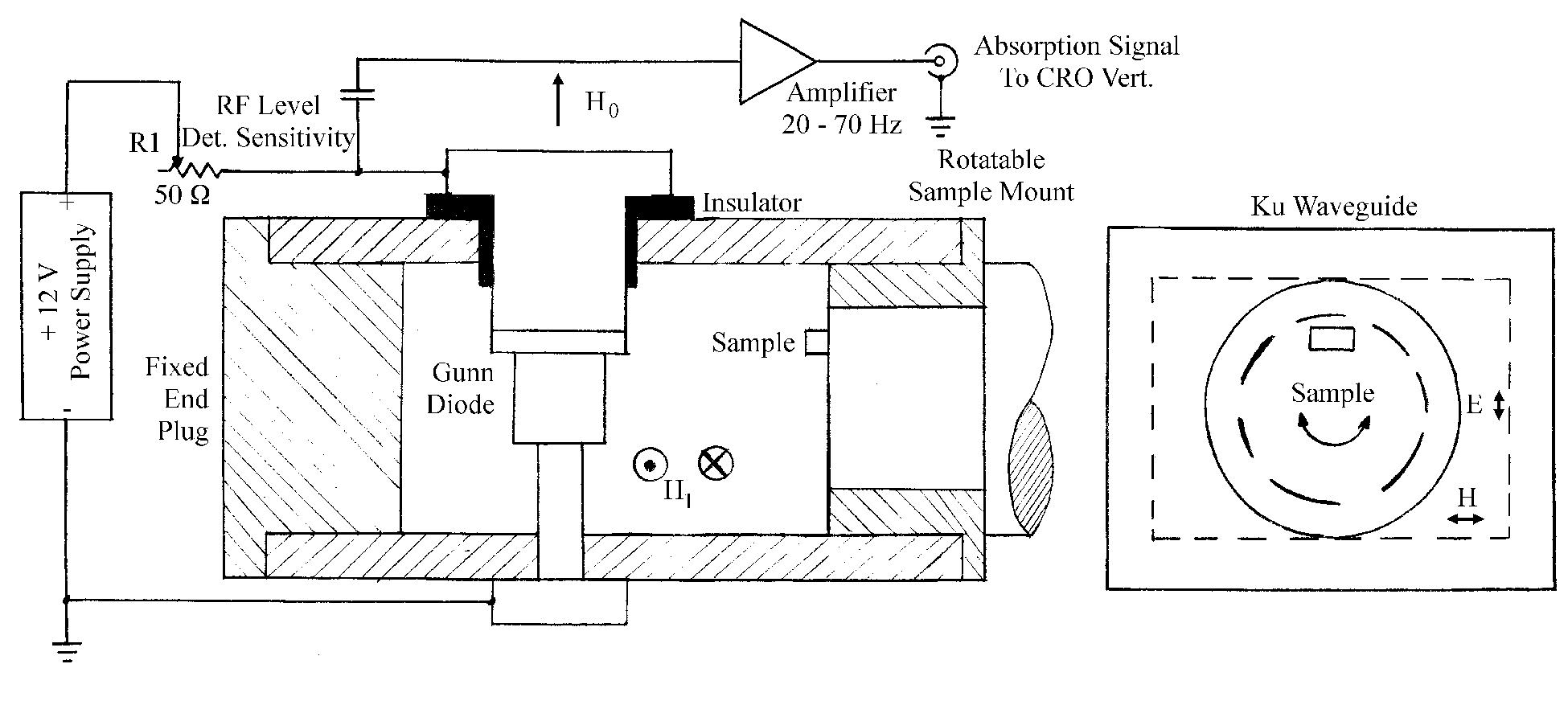
Figure 3. The Microwave Generator/Detector components.
A Gunn diode displays conductivity that is non-linear with applied voltage; i.e., it has a negative-resistance V/I characteristic.
Figure 4. Characteristic V/I curve for a negative-resistance device (Gunn diode).
The diode contains an extremely thin P-N junction diffused into a heavily doped GaAs (Gallium Arsenide) substrate. The frequency of oscillation is determined by the very high mobility of the electron/hole carriers in GaAs, and the thickness of the junction. A benefit of the very thin junction (10^-3cm) is that the conduction electrons are minimally affected by large magnetic fields (4-5 kG).
The diode is powered by a stable regulated power supply and R1, a series ten-turn variable 50 Ohm resistor. When Rl is set to its maximum (cw), the operating point is to the left of the Peak Point. As this resistance is reduced, the operating point moves to the right of the Peak Point into the negative-resistance region where a microwave frequency of extreme spectral purity is generated. Further reduction in series resistance increases the power.
Because the Gunn diode acts simultaneously as both source and detector of microwaves, optimization of the Signal-to-Noise Ratio is an interdependent exercise. Both the level of microwave fields generated and the detection sensitivity are affected by Rl. A 60 Hz signal, produced by the reduction of the cavity Q when a sample absorbs energy at resonance (a reduction in the microwave field level), is detected by the diode, and amplified by a low-noise amplifier used to drive the vertical display of the CRO. Detection sensitivity will be greatest when the operating point is "marginal", just to the right of the Peak Point. The optimum requires operation a bit farther into the negative-resistance region.
Samples in the cavity are DPPH plus trace quantities of several ions of the 3d series (Mn++ and either Cr+++ or Fe+++) diffused into a carrier lattice of crystalline MgO (Magnesium Oxide). The field for one of the resonances depends slightly upon the orientation of the crystal of MgO with respect to the magnetic field. Can you suggest a reason for this?
1. First set the 60 Hz modulation at maximum, and preset Rl to its CLOCKWISE stop (maximum value of 50 Ohm). Force the diode to oscillate by slowly rotating Rl COUNTER CLOCKWISE, i.e., reduce the value of Rl. The onset of oscillations will be indicated by an abrupt jump of the trace on the CRO. Sometimes the narrow trace will suddenly be replaced by a broad vertical band of low-frequency waveforms ("squegging"). If the latter are seen, you have set the operating point almost exactly on the peak point. Increase the level of oscillations slightly to restore a thin trace with a bit of "grass" growing on it (thermal noise), then slowly raise the magnet current until you locate the large DPPH peak and then readjust the diode bias to get the best S/N. Note the effect of varying the modulation amplitude and phase. Why are two peaks seen?
2. Use the Hall probe to measure H_0 with the DPPH peak centered on the trace, then calculate the frequency of the microwaves by using the g-factor for DPPH (2.0038). Measure and explain the width of the signal. (The Hall probe operating current has been set to make the system direct reading, with an absolute accuracy of ( < 3%. When the DMM is set to its 200 mV range, the least significant digit will equal 1 Gauss (ignore the decimal point). The Hall device has a substantial temperature coefficient (~ -0.1%/Co), and should be exposed to the warm magnet pole caps for the shortest practical time, and then removed to allow it to return to "room temperature".
3. Measure the magnetic fields required to center all other peaks on the CRO. Six are due to Mn++ while the others are due to either Cr+++ or Fe+++. Try to determine which of the peaks are due to Cr+++ or Fe+++. You will require a knowledge of the electron configuration of both ions in order to do this (the 'g' factor for Cr+++ in MgO is 1.9800 ± 0.0063; and for Fe+++, 'g' = 2.0037 ± 0.0007).
* Primary reference.
